Sketch
If the characteristics of a data stream changes, the statistical model represented by the probability distribution for the data stream should be modified, too. We propose the Sketch, which is an online algorithm that can estimate distribution for both stationary and non-stationary data streams, with high speed and high accuracy using only limited memory. We evaluate the performance and characteristics of Sketch over various types of stationary and non-stationary data streams. The experimental results show that Sketch exhibits significantly improved speed compared with its alternatives. The results also demonstrate that Sketch adapts well to various non-stationary data streams. As many data streams in the real world are non-stationary, we believe that Sketch can be widely used for many statistical algorithms processing such data streams.
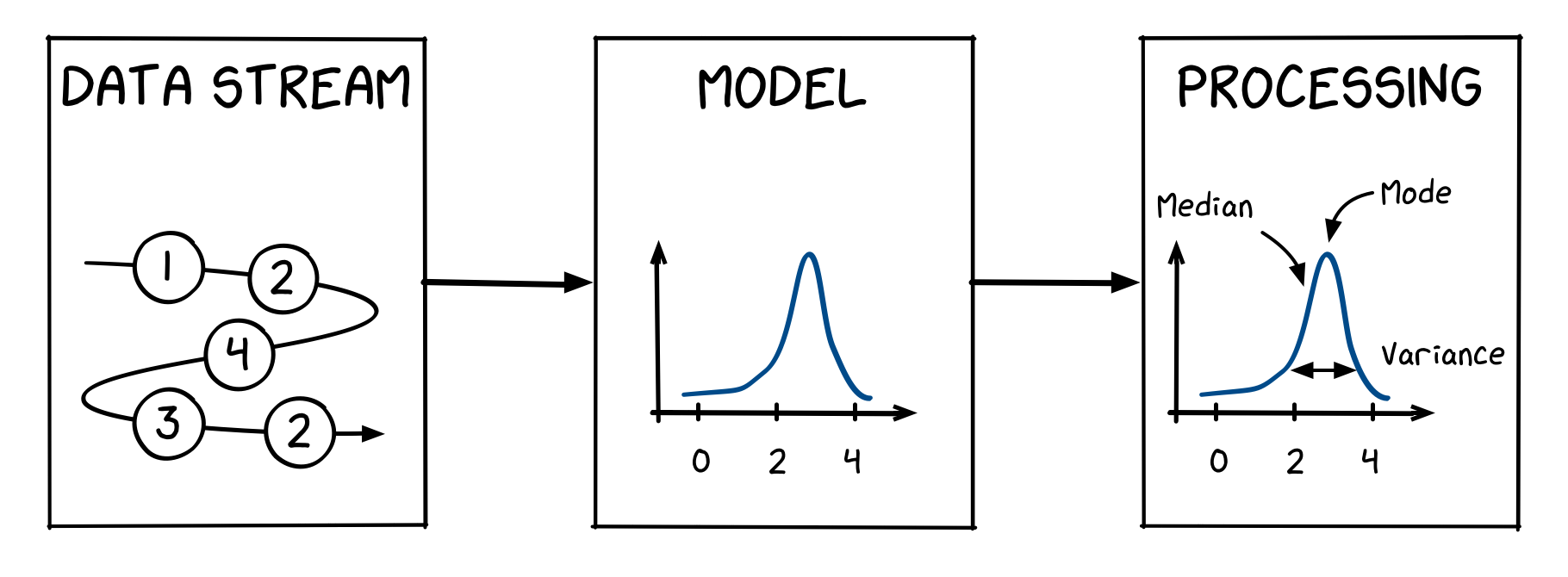
Quick Start
First, let’s create a data stream by randomly extracting 100 data from the standard normal distribution $\mathcal {N} (0, 1)$ with an mean of 0 and a variance of 1.
val underlying = NumericDist.normal(0.0, 1.0)
val (_, samples) = underlying.samples(100)
Now, construct a model that reflects the data stream using Sketch data structure. The code below shows that creates an empty model (called sketch0) with no data recorded, and records the data stream that we created earlier. After the data stream is recorded, the Sketch model is updated with the model that reflects the data stream (called sketch1).
val sketch0 = Sketch.empty[Double]
val sketch1 = samples.foldLeft(sketch0) {
case (sketch, sample) => sketch.update(sample)
}
Then, get various statistics from sketch1, a model that represents the previously obtained data stream. The code below shows an operation that takes four different statistical features from sketch1. First, we get the probability of a certain interval from sketch1. Second, we get the median of sketch1. Third, we extract the sample from sketch1. Last, we measure the Kullback-Leibler divergence between sketch1 and the underlying distribution–i.e. standard normal distribution.
// Estimated Pr(0.0 ≤ x ≤ 1.0)
val prob = sketch1.probability(0.0, 1.0)
// Estimated median
val median = sketch1.median
// Sample from sketch
val sample = sketch1.sample._2
// KL-divergence
val kld = KLD(underlying, sketch1)
In addition to the various operations introduced here, Sketch can be used to perform online statistical processing on various datasets and data streams.
Build and Update the Model using Sketch
There are two ways to construct Sketch. First, create a Sketch with nothing recorded. This method is used when no prior knowledge is given from the data stream. Or, build the most appropriate Sketch from a given dataset. This method is used when batching a dataset, or when a prior knowledge is given.
// build an empty model
val emptySketch = Sketch.empty[Double]
// build a model for given dataset-list of (variable, count)
val dataset = (0.2, 1.0) :: (-0.1, 1.0) :: (1.8, 1.0) :: (1.1, 1.0) :: Nil
val concatSketch = Sketch.concat(dataset)
If the data is given consecutively, the Sketch (assigned to sketch) created above should be updated to reflect the new data. This process is important when the data stream is non-stationary.
// update sketch for the new data 0.5
sketch.update(0.5)
How it works
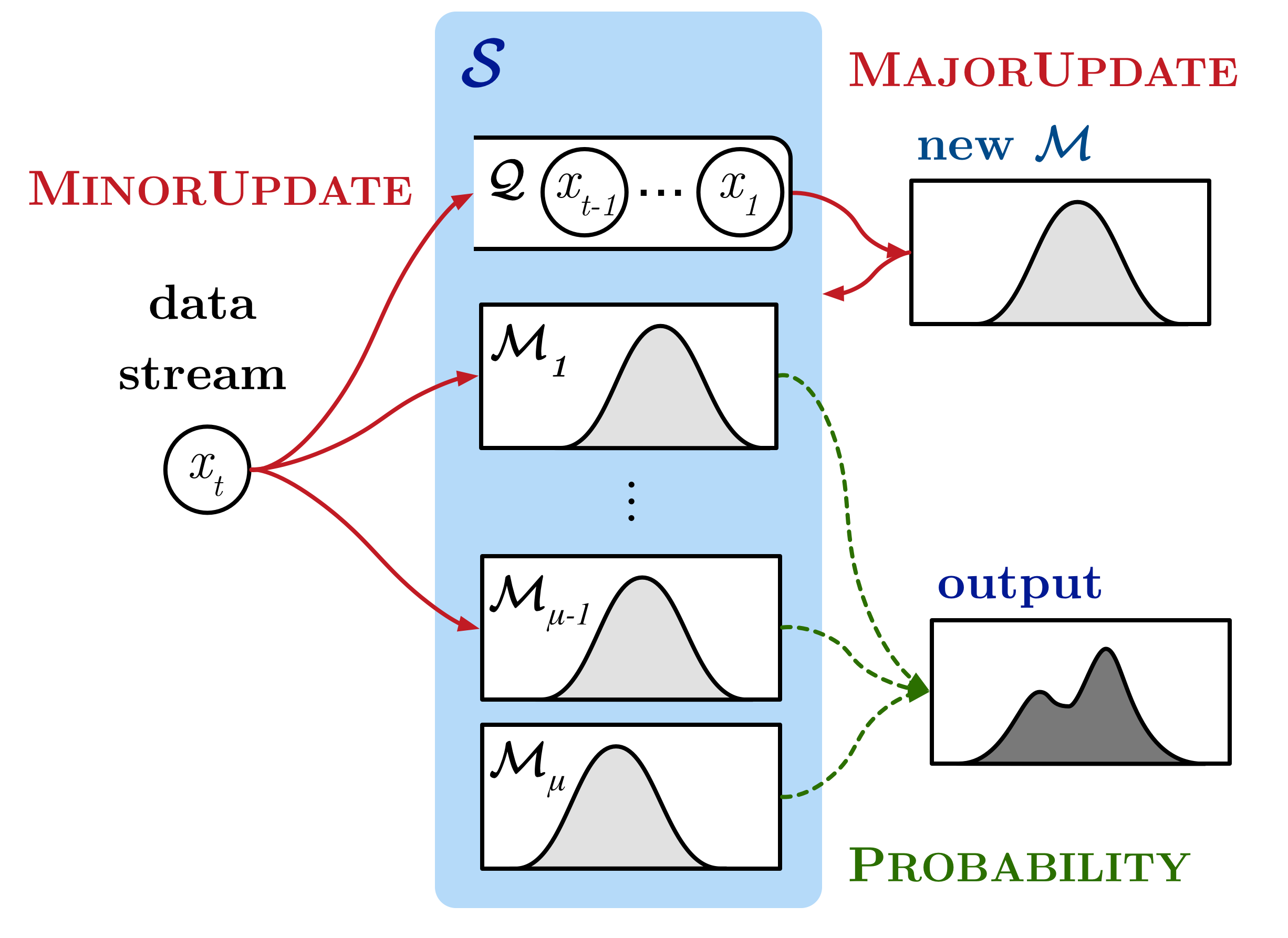
The Sketch framework contains two algorithms. One algorithm is used to update Sketch for the dataset online (i.e., update). The other algorithm is used to query the PDF from Sketch (i.e., probability). Meanwhile, Sketch data structure is a set of models. Thus, the update and probability algorithms for Sketch are equivalent to the combination of update and probability algorithms for the models that are elements of Sketch.
To define update and probability for Sketch, we introduce four elementary operations—minorUpdate, majorUpdate, diagnose, and probability. The type signatures of these operations are as follows:
def minorUpdate[A](sketch: Sketch[A], as: List[(A, Count)]): Sketch[A]
def majorUpdate[A](sketch: Sketch[A], as: List[(A, Count)]): (Sketch[A], Option[Histogram[Double]])
def diagnose[A](sketch: Sketch[A]): Boolean
def probability[A](sketch: Sketch[A], start: A, end: A): Double
There are two types of operations updating Sketch. The first operation is minorUpdate. This operation updates all models in Sketch for given data. Subsequently, it temporarily stores the data in queue. The other operation is majorUpdate. This operation builds a new model based on both dataset in the queue and models in Sketch, and it enqueues the new model to Sketch. Subsequently, the operation dequeues an outdated model that was included in Sketch from Sketch .
Specifically, Sketch performs minorUpdate to update Sketch for data. If the size of the queue is greater than the given parameter, Sketch diagnoses whether Sketch adapts well to the queue by comparing Sketch and the queue. When the result of diagnose is true, Sketch performs majorUpdate to update Sketch for the queue.
Analyze the Model
Get various statistical characteristics from Sketch, a model that represents the previously obtained datasets and data streams. The code below shows an operation that takes four different statistical features from Sketch that is assigned to sketch. First, we get the probability of a certain interval from sketch. Second, we get the median of sketch. Third, we extract the sample from sketch. Last, we measure the Kullback-Leibler divergence between sketch and the underlying distribution.
// Estimated Pr(0.0 ≤ x ≤ 1.0)
val prob = sketch.probability(0.0, 1.0)
// Estimated median
val median = sketch.median
// Sample from sketch
val sample = sketch.sample._2
// KL-divergence
val kld = KLD(underlying, sketch)
Full analysis method
WIP
Configuration
Parameters of Sketch
Sketch takes four regular independent parameters:
-
cmapNois the maximum number of models in the data structure of theSketchframework. -
thresholdPeriodis the maximum size of the buffer in the data structure ofSketchframework. Further, theupdateoperation ofSketchperformsdiagnoseevery number ofthresholdPeriods. -
decayFactoris a factor used to forget the past contributions of data when performing theprobabilityquery operation inSketch. -
rebuildThresholdis a threshold for minor and major concept drifts. When major concept drift occurs, themajorUpdateoperation, which updates the estimated PDF accurately but slowly, is performed.
Full parameters
WIP
Customizing Configuration
implicit val conf: SketchConf = SketchConf(
cmapNo = 10,
cmapStart = Some(-20),
cmapEnd = Some(20),
rebuildThreshold = 0.2,
startThreshold = 10,
thresholdPeriod = 30,
decayFactor = 2
)
val sketch0 = Sketch.empty[Double]