Experiments

We measure the computation time, memory usage, and accuracy of the Sketch for various types of stationary and non-stationary data streams. Subsequently, we compare these results with those of the existing density estimation algorithms such as SPDT and oKDE. Here, oKDE is based on the kernel method implemented in Java and SPDT is based on a histogram implemented in Scala. The results show that Sketch requires less computation time than the alternatives for both stationary and non-stationary data stream and it also adapts better for a non-stationary data streams.

Computing Platform

We performed all experiments on the following machine with 4-core Intel CPU i7-7700K @ 4.2 GHz and 16 GB memory. The experiments run on a single thread.

Metrics

Throughput

We evaluate the computation times of update and probability operations of Sketch in million operations per second (Mops/s), which indicates the number of times per second our benchmark operation could be executed. There is a performance degradation in JVM in the first few iterations. To address this issue, we start to record its throughput after twenty warm-up phases. Subsequently, we record the arithmetic mean value of throughputs of the subsequent thirty measurement phases to minimize the accidental deviation.

Memory Usage

The PDF estimated using the density estimation algorithm continues to use memories. After the estimation, this result or its changing history is recorded in the disk if necessary. Therefore, we record only the memory usage of the estimated PDF, but not the whole memory usage consumed by the update or probability operation.

Statistical Distance

We measure the discrepancy between the estimated PDF and the underlying distribution for a data stream. Although there are many matrices, we adopt average error.

Restoring and Resistance Coefficients

We introduce damped harmonic oscillator model for unit mass to represent the characteristics of the density estimation algorithms when concept drift occurs.

$\ddot{D_\Delta} + \underbrace{c \cdot \dot{D_\Delta}}_{\text{Resistance term}} + \underbrace{k \cdot D_\Delta}_{\text{Restoring term}} = 0$

where $D_\Delta$ is the statistical distance, $\dot{D_\Delta}$ and $\ddot{D_\Delta}$ are the first- and second-order time derivatives of $D_\Delta$ or velocity and acceleration of $D_\Delta$, respectively, $c$ is the resistance coefficient, and $k$ is the restoring coefficient.

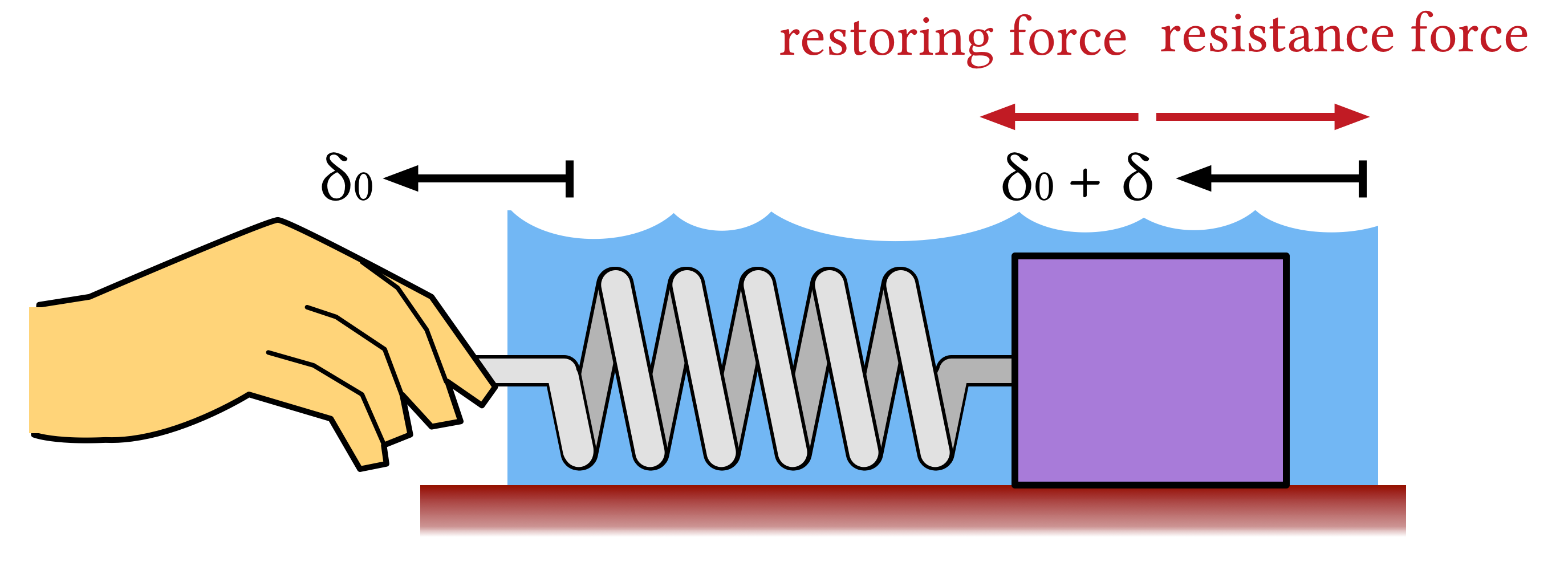
infographic

This model is an equation of motion for an object subject to viscous resistive force (caused by the stability for outliers) and restoring force (caused by the update operation) following Hooke’s law in a space of $D_\Delta$. For simplicity, we linearly approximate the restoring force for the distance and the resistive force for the velocity in first-order. We select the coefficients so that the harmonic oscillator model has the best fit to the measured $D_\Delta$. The higher the selected $k$, the better the estimated PDF adapts to the data stream with concept drift. The higher the selected $c$, the slower the estimated PDF adapts to the data stream with concept drift and the more stable the estimated PDF when an outlier occurs.